Number System : Arithmetic Progression and Geometric Progression

Hello Friends! 

Under this post " Number System: Arithmetic Progression and Geometric Progression " we will see arithmetic progression and geometric progression, formula used for AP and GP and types of questions asked in competitive exams.

1) Geometric Progression / Geometric Series / Geometric Sequence : x, xr, xr², xr³, xr⁴, --- are said to be in geometric progression. Here, a is first term and r is common ratio. 

a) n^th term = xr ^{(n -1)}

b) Sum of n terms =	x (1 – rn)	, here r < 1
	(1 – r)

c) Sum of n terms =	x (rn – 1)	, here r > 1
	(r – 1)

2) Arithmetic Progression / Arithmetic Series / Arithmetic Sequence : x, x + y, x + 2y, x + 3y are said to be in A.P. Here x is first term and common difference is y.


a) n^th term = x + (n – 1) y

b) Sum of n terms =	n	[2x + (n – 1)y]
	2

3) 1 + 2 + 3 +- - - - + n =	n(n + 1)
	2

4) (12 + 22 + 32 - - - - + n2) =	n(n + 1) (2n + 1)
	6

5) (13 + 23 + 33 - - - - + n3) =		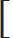n(n + 1)		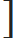2
		2

At last, A special thanks to choose LOUD STUDY.

If you have any doubts or confusion, please comment in the comment box below, we will try to reply you as soon as possible.